Πρόβλεψη Περιουσιακών Στοιχείων Επιχειρήσεων: Η Μέθοδος της Γραμμικής Παλινδρόμησης

Η μέθοδος της παλινδρόμησης είναι μια στατιστική μέθοδος. Για τη χρησιμοποίηση του μοντέλου της απλής γραμμικής παλινδρόμησης γίνεται η αποδοχή ότι υπάρχει μια θεμελιώδης σχέση ανάμεσα σε δύο μεταβλητές και ότι αυτή η σχέση μπορεί να παρουσιαστεί με μια ευθεία γραμμή.

Γράφει ο Καθηγητής Κωνσταντίνος Ζοπουνίδης, Ακαδημαϊκός, Βασιλική Ακαδημία Οικονομικών και Χρηματοοικονομικών, Βασιλική Ευρωπαϊκή Ακαδημία των Διδακτόρων, Πολυτεχνείο Κρήτης & Audencia Business School, France

Διαβάστε Επίσης

Διάκριση του Καθηγητή Ακαδημαϊκού Κωνσταντίνου Ζοπουνίδη

Nov 13, 2024

Τεχνητή Νοημοσύνη και ESG

Oct 8, 2024

Ο μαθηματικός τύπος του μοντέλου είναι:

Υ = f(X)

και

Υ = α + bX

Όταν Χ = 0, Υ = α, α είναι το σημείο όπου η ευθεία γραμμή τέμνει τον άξονα Υ.

Η τιμή του b ονομάζεται συντελεστής της παλινδρόμησης και δείχνει τη μεταβολή του Υ που προκύπτει από μια μεταβολή του Χ ίση με τη μονάδα. Το b μετρά επίσης την κλίση της ευθείας γραμμής.

Πριν υπολογιστούν οι διάφοροι παράμετροι του μοντέλου, είναι καλό να τονιστούν τα κύρια πλεονεκτήματα και μειονεκτήματα της μεθόδου.

Πλεονεκτήματα

• Είναι μια μέθοδος που μετρά την αιτιότητα όπως και οι μέθοδοι που χρησιμοποιούνται στις χρονολογικές σειρές.
• Η μέθοδος της γραμμικής παλινδρόμησης χρησιμοποιεί ένα στατιστικό μοντέλο και κατά συνέπεια είναι δυνατό να εκτιμηθεί η ακρίβειά του με στατιστικές μετρήσεις.

Μειονεκτήματα

• Βρίσκονται κυρίως στη γραμμικότητα των σχέσεων. Επίσης η χρησιμοποίηση της μεθόδου απαιτεί πολλά δεδομένα για να φθάσει σε αποτελέσματα που είναι στατιστικώς σημαντικά

Προσδιορισμός των παραμέτρων

Ο προσδιορισμός των παραμέτρων του μοντέλου γίνεται με τη μέθοδο των ελαχίστων τετραγώνων. Ο σκοπός μας εδώ δεν είναι να γίνει μια αναλυτική περιγραφή (η όλη διαδικασία υπολογισμού μπορεί να βρεθεί μέσα σε οποιοδήποτε βιβλίο στατιστικής), αλλά απλώς να δοθούν οι μαθηματικοί τύποι που θα διευκολύνουν τη χρησιμοποίηση του μοντέλου.

Έχουμε το μοντέλο Y = α + bX

Όπου Υ = η μεταβλητή υπό πρόβλεψη,

Και Χ = η μεταβλητή βάσει της οποίας θα γίνει η πρόβλεψη του Υ

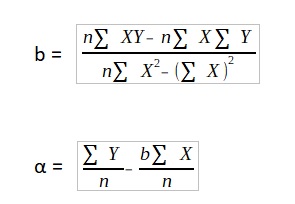
ή

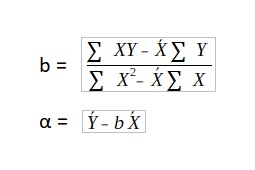
Ο συντελεστής συσχέτισης R επιτρέπει τη μέτρηση του βαθμού εξάρτησης της μεταβλητής Y από τη μεταβλητή Χ. Ο συντελεστής συσχέτισης είναι ίσος με την τετραγωνική ρίζα του συντελεστή προσδιορισμού. Και ο συντελεστής προσδιορισμού ισούται με:

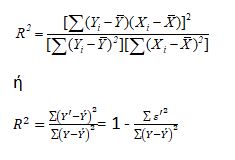
Ένα παράδειγμα

Θα χρησιμοποιηθεί τώρα η μέθοδος της απλής γραμμικής παλινδρόμησης στην πρόβλεψη των χρηματοδοτικών αναγκών της επιχείρησης. Πιο συγκεκριμένα θα εξεταστεί η σχέση μεταξύ των αποθεμάτων και των πωλήσεων μιας επιχείρισης Ω για την περίοδο 1978-1987. Στην περίπτωση αυτή η προβληματική είναι να προβλεφθεί το ύψος των αποθεμάτων δεδομένου του προβλεπόμενου αριθμού πωλήσεων για την περίοδο μετά το 1987. Το πρόβλημά μας είναι λοιπόν να κατασκευάσουμε ένα μοντέλο πρόβλεψης με τη βοήθεια της απλής γραμμικής παλινδρόμησης, με βάση τα δεδομένα της περιόδου 1978-1987 και μετά να επεκτείνουμε (extrapolation) το μοντέλο μέσα στο χρόνο πέραν του 1987.

Τα δεδομένα του προβλήματος παρουσιάζονται στον παρακάτω πίνακα:

Χρησιμοποιώντας τους ανωτέρω τύπους καταλήγουμε στα ακόλουθα αποτελέσματα:

α = 168,285
b = 0,04987

R² = 0,9496
R = 0,9745
Σ Χ= 131194

Χ = 13119,4

Σ Χ² = 2268824400
(Σ Χ)² = 17211866000
Σ ΧΥ = 135233010
Σ Υ = 8226
Υ = 822,6

Το μοντέλο πρόβλεψης που υπολογίστηκε από τη μέθοδο της απλής γραμμικής παλινδρόμησης είναι:

Υ = 168,3 + 0,05Χ

Η γραμμή παλινδρόμησης παρουσιάζεται στο Σχήμα 1. Όπως φαίνεται όλα τα σημεία βρίσκονται σχετικά κοντά στη γραμμή παλινδρόμησης που υπολογίσθηκε:
Ο συντελεστής συσχέτισης R μεταξύ των πωλήσεων και των αποθεμάτων για τα στοιχεία της επιχείρησης Ω είναι αρκετά υψηλός 0,9745, γεγονός που δείχνει ότι η διασπορά των πραγματικών δεδομένων γύρω από τη γραμμή παλινδρόμησης είναι σχετικά μικρή.

Σχήμα 1: Γραφική αναπαράσταση του μοντέλου παλινδρόμησης για την πρόβλεψη των αποθεμάτων βάσει των πωλήσεων

Επέκταση του μοντέλου πρόβλεψης

Αρχικά γίνεται η υπόθεση ότι, σύμφωνα με τις προβλέψεις που έγιναν, οι πωλήσεις της Ω μέχρι το 1991 θα αυξηθούν με τον ίδιο ρυθμό της περιόδου 1983-1987, δηλαδή περίπου κατά 35%. Αυτή η πρόβλεψη θα έδινε για το 1991 πωλήσεις ύψους 32.476 εκατ. ευρώ. Βέβαια μια πρόβλεψη των πωλήσεων για το 1991 θα απαιτούσε μια πολύ εμπεριστατωμένη μελέτη δεδομένου της αβεβαιότητας που υπάρχει στη διεθνή αγορά. Αλλά εδώ το ενδιαφέρον μας είναι να αναπτυχθούν σχέσεις μεταξύ των πωλήσεων και των αποθεμάτων.

Έτσι, είναι δυνατό να προβλεφθεί το ύψος των αποθεμάτων για διάφορα επίπεδα πωλήσεων με τη βοήθεια της απλής γραμμικής παλινδρόμησης.

Αν οι προβλεπόμενες πωλήσεις της Ω για το 1991 είναι 32476 εκατ. ευρώ, το ύψος των προβλεπόμενων αποθεμάτων με βάση το μοντέλο πρόβλεψης θα είναι 1,792 εκατ. ευρώ. Αν χρησιμοποιηθεί ο χαμηλός δείκτης του 1987 που είναι περίπου 5% θα έχουμε 32.476×0,05 = 1.624) μια πρόβλεψη κατά 168 εκατ. ευρώ χαμηλότερη από αυτή που προέρχεται από τη μέθοδο της απλής γραμμικής παλινδρόμησης.

Πρέπει να σημειωθεί ότι η χρήση της μεθόδου της γραμμικής παλινδρόμησης όπως αυτή εφαρμόζεται στο λογαριασμό αποθέματα, μπορεί να χρησιμοποιηθεί για την πρόβλεψη οποιουδήποτε άλλου λογαριασμού του ισολογισμού, των αποτελεσμάτων χρήσης, καθώς και άλλων οικονομικών καταστάσεων.

Συμπερασματικά, μπορεί να αναφερθεί ότι και οι δύο μέθοδοι του Ποσοστού των Πωλήσεων και της Γραμμικής Παλινδρόμησης είναι απλές και μπορούν να εφαρμοστούν χωρίς δαπάνη. Οι μέθοδοι αυτές δίνουν μια καλή βάση για την αναθεώρηση και τον έλεγχο των πιο σύνθετων και αναλυτικών μεθοδολογιών που μπορούν να χρησιμοποιηθούν.