Το υπόδειγμα αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων αναπτύχθηκε από τους Sharpe (1964), Lintner (1965) και Moussin (1966), (βλ. Ξυδώνας, Ψαρράς, Ζοπουνίδης, Σύγχρονη Θεωρία Χαρτοφυλακίου, Εκδ. Κλειδάριθμος, 2010).
Γράφει ο Καθηγητής Κωνσταντίνος Ζοπουνίδης, Ακαδημαϊκός, Βασιλική Ακαδημία Οικονομικών και Χρηματοοικονομικών, Βασιλική Ευρωπαϊκή Ακαδημία των Διδακτόρων, Πολυτεχνείο Κρήτης & Audencia Business School
Μαθηματική ανάπτυξη
Οι υποθέσεις του υποδείγματος έδειξαν ότι ο επενδυτής οφείλει να παίρνει υπόψη του, σε ότι αφορά αποφάσεις επένδυσης σε περιουσιακά στοιχεία, το περιουσιακό στοιχείο με απόδοση χωρίς κίνδυνο Από στατιστική πλευρά, ένα χρεόγραφο χωρίς κίνδυνο (έστω Χ1) έχει τα ακόλουθα χαρακτηριστικά:
![]()
Στη συνέχεια δύο περιπτώσεις θα εξεταστούν:
- στην πρώτη, ο επενδυτής θα κατασκευάσει ένα χαρτοφυλάκιο που θα αποτελείται από το χρεόγραφο χωρίς κίνδυνο και ένα επικίνδυνο χρεόγραφο,
- στη δεύτερη, ο επενδυτής θα κατασκευάσει ένα χαρτοφυλάκιο που θα αποτελείται από το χρεόγραφο χωρίς κίνδυνο και το χαρτοφυλάκιο όλων των επικίνδυνων χρεογράφων (Market Portfolio).
Η δεύτερη αυτή περίπτωση θα δώσει τον τελικό τύπο του υποδείγματος αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων.
1η περίπτωση: επιλογή του επενδυτή ανάμεσα στο χρεόγραφο χωρίς κίνδυνο και ένα επικίνδυνο χρεόγραφο
Έστω οι ακόλουθοι συμβολισμοί:
Rf = το χρεόγραφο χωρίς κίνδυνο
A = το επικίνδυνο χρεόγραφο
a = το ποσοστό του επικίνδυνου χρεογράφου μέσα στο χαρτοφυλάκιο
1–a = το ποσοστό του χρεογράφου χωρίς κίνδυνο μέσα στο χαρτοφυλάκιο.
Η αναμενόμενη απόδοση και ο κίνδυνος του χαρτοφυλακίου προσδιορίζονται ως εξής:

οπότε η τυπική απόκλιση ισούται με:

Η τοποθέτηση του παραπάνω τύπου στον τύπο (1) δίνει το ακόλουθο αποτέλεσμα:

Η παραπάνω σχέση είναι η εξίσωση μιας ευθείας που αρχίζει από το Rf και περνά από το Α (βλ. Σχήμα 1).
Στο σημείο Α, a = 1, οπότε σ(Rρ) = σA και η σχέση (4) διαμορφώνεται ως εξής: E(Rp) = Rf + E(A) – Rf = Ε(Α).
Από το Σχήμα 1 εξάγονται τα ακόλουθα συμπεράσματα.
- στο διάστημα της ευθείας RfΑ , ο επενδυτής κατανέμει τα κεφάλαια του ανάμεσα στο επικίνδυνο χρεόγραφο και στο χρεόγραφο χωρίς κίνδυνο,
- στο διάστημα της ευθείας πέρα από το Α, ο επενδυτής δανείζεται κεφάλαια με επιτόκιο ίσο με την απόδοση του χρεογράφου χωρίς κίνδυνο και τα επενδύει μέσα στο επικίνδυνο χρεόγραφο (πρόκειται για επενδυτή που “αγαπά” τον κίνδυνο).
Οι παραπάνω σχέσεις δείχνουν ότι η αναμενόμενη απόδοση και ο κίνδυνος είναι γραμμικές συναρτήσεις του ποσοστού a που επενδύεται μέσα στο επικίνδυνο χρεόγραφο.
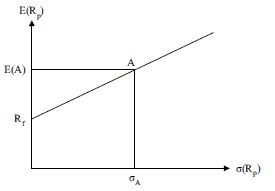
Σχήμα 1: Η γραμμή του επικίνδυνου χρεογράφου Α
2η περίπτωση: επιλογή του επενδυτή ανάμεσα στο χρεόγραφο χωρίς κίνδυνο και το χαρτοφυλάκιο όλων των επικίνδυνων χρεογράφων (Market Portfolio)
Στην περίπτωση αυτή τίθεται το θεώρημα του διαχωρισμού (separation theorem). Σύμφωνα με το θεώρημα αυτό κάθε επενδυτής προσπαθεί να μεγιστοποιήσει τη χρησιμότητα του χαρτοφυλακίου του το οποίο είναι ένας συνδυασμός του χρεογράφου χωρίς κίνδυνο και ενός χαρτοφυλακίου επικίνδυνων χρεογράφων το οποίο προσδιορίζεται από τη γραμμή που αρχίζει από το χρεόγραφο χωρίς κίνδυνο και εφάπτεται του αποτελεσματικού συνόλου των επικίνδυνων χρεογράφων.
Η ευθεία γραμμή RfΜΝ είναι το αποτελεσματικό σύνολο για όλους τους επενδυτές. Μ είναι το χαρτοφυλάκιο αγοράς όλων των επικίνδυνων χρεογράφων (the market portfolio of all risky assets).
Η ευθεία γραμμή RfΜΝ ονομάζεται γραμμή κεφαλαιαγοράς (Capital Market Line). Αρχίζει από το χρεόγραφο χωρίς κίνδυνο Rf και η κλίση της (the slope of the line) είναι ίση με [Ε(RΜ) – Rf]/σ(RΜ). Η εξίσωση της γραμμής κεφαλαιαγοράς είναι η ακόλουθη:

Η γραμμή αυτή προσφέρει μια απλή γραμμική σχέση ανάμεσα στην αναμενόμενη απόδοση και στον κίνδυνο για όλα τα αποτελεσματικά χαρτοφυλάκια χρεογράφων.
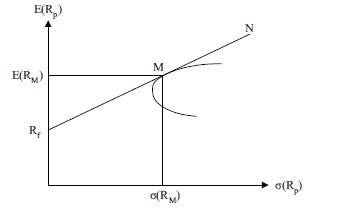
Σχήμα 2: Το αποτελεσματικό σύνολο για όλους τους επενδυτές και το χαρτοφυλάκιο αγοράς όλων των επικίνδυνων χρεογράφων
Το υπόδειγμα αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων στηρίζεται πάνω στη γραμμική αυτή σχέση και θέτει σε συσχέτιση την απόδοση ενός χαρτοφυλακίου αγοράς όλων των επικίνδυνων χρεογράφων.
Η μαθηματική απόδειξη της εξίσωσης του υποδείγματος είναι η ακόλουθη.
Έστω ένα χαρτοφυλάκιο που αποτελείται από:
- a% επενδύεται στο επικίνδυνο χρεόγραφο I
- (1 – a)% επενδύεται στο χαρτοφυλάκιο αγοράς Μ
Όταν η κεφαλαιαγορά (financial market) βρίσκεται σε ισορροπία δεν υπάρχει πλεόνασμα ζήτησης για κανένα επικίνδυνο χρεόγραφο. Συνεπώς κάθε εμπορεύσιμο χρεόγραφο κατέχει ένα ποσοστό αξίας μέσα στη συνολική αξία του χαρτοφυλακίου αγοράς. Μαθηματικά αυτό εκφράζεται:

Όπου Vi = η αξία αγοράς του επικίνδυνου χρεογράφου i,
ε Vi = η συνολική αξία αγοράς όλων των επικίνδυνων χρεογράφων,
και wi = το βάρος του επικίνδυνου χρεογράφου i μέσα στο χαρτοφυλάκιο αγοράς.
Υπολογίζονται τώρα η αναμενόμενη απόδοση και ο κίνδυνος του χαρτοφυλακίου.
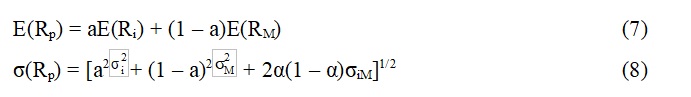
Οι ποικίλοι συνδυασμοί του επικίνδυνου χρεογράφου i και του χαρτοφυλακίου αγοράς Μ σχηματίζουν ένα σύνολο που παρουσιάζεται στο Σχήμα 3 με την καμπύλη I΄MI.
Σε συνάρτηση μιας δεδομένης μεταβολής του ποσοστού a που έχει επενδυθεί στο χρεόγραφο i, οι μεταβολές της αναμενόμενης απόδοσης και του κινδύνου του χαρτοφυλακίου προσδιορίζονται από τις παραγώγους των σχέσεων (7) και (8).


Σε κατάσταση ισορροπίας της κεφαλαιαγοράς, το χαρτοφυλάκιο αγοράς περιλαμβάνει ήδη το επικίνδυνο χρεόγραφο i με το ποσοστό wi. Άρα προκύπτει ότι το ποσοστό a είναι ένα πλεόνασμα ζήτησης του χρεογράφου i και είναι γνωστό ότι όταν υπάρχει ισορροπία στην κεφαλαιαγορά το πλεόνασμα ζήτησης πρέπει να είναι ίσο με μηδέν.
Θέτοντας a=0, οι σχέσεις (9) και (10) διαμορφώνονται ως εξής:
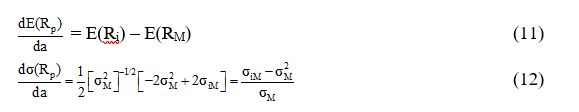
Ο λόγος των δύο σχέσεων (11) και (12) δίνει το ποσοστό παραχωρήσεων ανάμεσα στην αναμενόμενη απόδοση και στον κίνδυνο (return–risk trade–off) πάνω στην καμπύλη I΄MI (βλ. Σχήμα 3).
Το ποσοστό αυτό είναι ίσο με την κλίση της εφαπτομένης στο σημείο Μ:

Όταν η κεφαλαιαγορά βρίσκεται σε ισορροπία, η κλίση της γραμμής κεφαλαιαγοράς (βλ. εξίσωση 5) και η κλίση της εφαπτόμενης στο σημείο Μ πρέπει να είναι ίσες. Η εξίσωση των δύο σχέσεων δίνει τον μαθηματικό τύπο του υποδείγματος αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων.
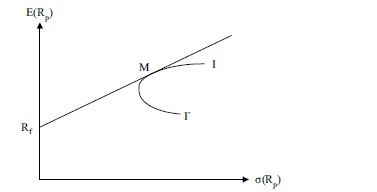
Σχήμα 3: Γραμμή κεφαλαιαγοράς και ποσοστό παραχωρήσεων πάνω στην καμπύλη Ι΄ΜΙ

Η σχέση (14) δείχνει ότι η αναμενόμενη απόδοση ενός επικίνδυνου χρεογράφου, E(Ri), είναι ίση με την απόδοση ενός χρεογράφου χωρίς κίνδυνο συν ένα πριμ κινδύνου. Το πριμ κινδύνου εκφράζεται ως η τιμή κινδύνου η οποία πολλαπλασιάζεται με την ποσότητα κινδύνου. Η τιμή του κινδύνου είναι η διαφορά ανάμεσα στην αναμενόμενη απόδοση του χαρτοφυλακίου αγοράς και στην απόδοση του χρεογράφου χωρίς κίνδυνο, δηλαδή [E(RΜ) – Rf], ενώ η ποσότητα του κινδύνου, συχνά ονομάζεται βi, είναι ο τύπος:

Το χρεόγραφο χωρίς κίνδυνο έχει ένα β=0 διότι η συνδιακύμανση του με το χαρτοφυλάκιο αγοράς είναι ίση με μηδέν.
Για το χαρτοφυλάκιο αγοράς το β είναι ίσο με:
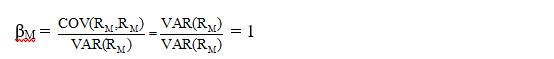
Το β ονομάζεται επίσης συστηματικός κίνδυνος ή κίνδυνος της αγοράς ή κίνδυνος μη διαφοροποιήσιμος. Μετρά το εύρος των αποδόσεων μιας συγκεκριμένης επένδυσης σε σχέση με τις αποδόσεις της αγοράς.
Το Σχήμα 4 παρουσιάζει τη σχέση αναμενόμενης απόδοσης ενός επικίνδυνου χρεογράφου (π.χ. μετοχής) και του συστηματικού της κινδύνου β όπως αυτή αναπτύχθηκε από το υπόδειγμα αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων.
Η εξίσωση (14) δύναται να παρουσιαστεί ως εξής:
E(Ri) = Rf + [E(RΜ) – Rf]βi (16)
Η χρησιμοποίηση της σχέσης (16) δείχνει καθαρά την επίδραση του συντελεστή β.
Όταν βi = 0 E(Ri) = Rf
Όταν βi = 1 E(Ri) = Ε(RΜ)
Όταν βi > 1 E(Ri) > Ε(RΜ)
Όταν βi < 1 E(Ri) < Ε(RΜ)
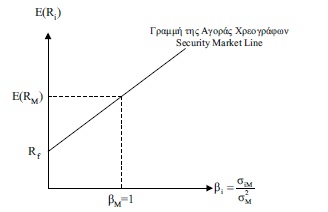
Σχήμα 4: Το υπόδειγμα Αποτίμησης Κεφαλαιουχικών Περιουσιακών Στοιχείων
Το υπόδειγμα αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων χρησιμοποιείται τόσο στη διαχείριση χαρτοφυλακίων όσο και στις χρηματοοικονομικές αποφάσεις χρηματοδότησης και επένδυσης (βλ. Hamada, 1969, Rubinstein, 1973 και Weston, 1973, βλ. Ζοπουνίδης, Βασικές Αρχές Χρηματοοικονομικού Μάνατζμεντ, Εκδ. Κλειδάριθμος, 2013).
Άσκηση
Είστε χρηματιστηριακός αναλυτής της New Bank. Το τμήμα χρηματοοικονομικής ανάλυσης σας δίνει τις ακόλουθες προβλέψεις:
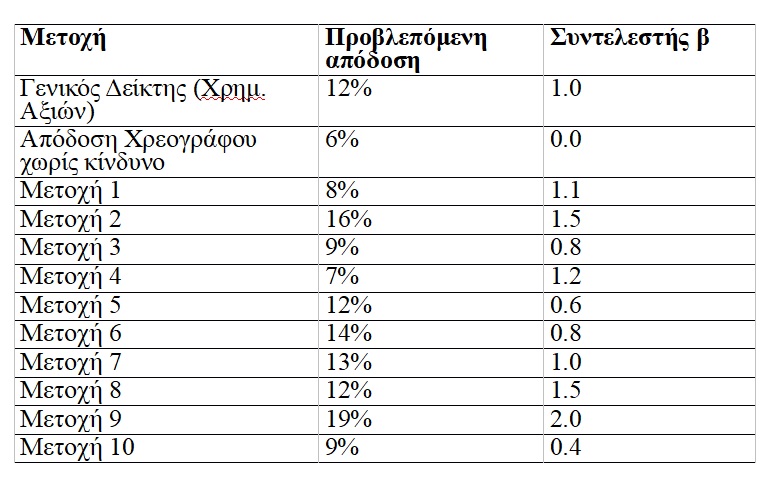
Χρησιμοποιώντας το Υπόδειγμα Αποτίμησης Κεφαλαιουχικών Περιουσιακών Στοιχείων, ποιες μετοχές θα προτείνατε για αγορά; Υπολογίστε επίσης την τιμή β του χαρτοφυλακίου με τις μετοχές που θα επιλέξετε.
Μεθοδολογία επίλυσης
Υπολογίζεται αρχικά η απαιτούμενη αποδοτικότητα
Μετοχή 1: 8=6+1.1[12-6]
8<12.6 (-4,6)
Μετοχή 2: 8=6+1.5[12-6]
(+1)
Μετοχή 3: 9=6+0.8[12-6]
9<10.8 (-1.8)
Μετοχή 4: (-6.2)
Μετοχή 5: (+2.4)
Μετοχή 6: (+3,2)
Μετοχή 7: (+1)
Μετοχή 8: (-3)
Μετοχή 9: (+1)
Μετοχή 10: (+0.6)
Με βάση τα αποτελέσματα της απαιτούμενης αποδοτικότητας ως προς την προβλεπόμενη, επιλέγονται οι μετοχές που έχουν θετικό πρόσημο, δηλαδή οι μετοχές 2,5,6,7,9,10.
Υπολογισμός του Beta του χαρτοφυλακίου
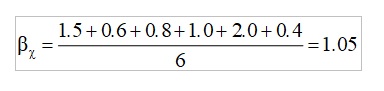


.gif?rand=5501)

















