Ασαφή Σύνολα για την Ανάλυση της Πτώχευσης των Επιχειρήσεων

των Δρ Λία Κρασαδάκη,Πολυτεχνείου Κρήτης, Εργαστήριο ΕΡΓΑΣΥΑ. Κ. Ζοπουνίδη, καθηγητή Πολυτεχνείου Κρήτης, Επίτιμος Διδάκτωρ, ΑΠΘ & Μ. Δούμπου, Καθηγητή Πολυτεχνείου Κρήτης

Η πτώχευση των επιχειρήσεων είναι ένα γνωστό ερευνητικό πρόβλημα που συνήθως αντιμετωπίζεται με διάφορα μεθοδολογικά εργαλεία (βλ. Ζοπουνίδης, 2013). Στο συγκεκριμένο άρθρο επανεξετάζεται τι μπορεί να κρύβουν πέντε χρηματοοικονομικοί δείκτες χρησιμοποιώντας ως εργαλείο ανάλυσης, τη μέθοδο της Ποιοτικής Συγκριτικής Ανάλυσης με χρήση ασαφών συνόλων (fs/QCA). Η μέθοδος αυτή είναι μια χρήσιμη προσέγγιση για την αναζήτηση αναγκαίων και ικανών συνθηκών (μεταβλητών ή συνδυασμών τους) για την παρουσία (ή την απουσία) ενός αποτελέσματος (πχ την πτώχευση). Όπως υποστηρίζει ο Woodside (2013), σε δεδομένα σύνολα αριθμών, ενδέχεται όλες οι παρατηρήσεις να μην υποστηρίζουν μια θετική ή μια αρνητική σχέση των ανεξάρτητων μεταβλητών (Χ) με την εξαρτημένη μεταβλητή (Υ). Ο ερευνητής χρησιμοποιώντας αυτή τη μέθοδο μπορεί να αυξήσει τη συμβολή της έρευνάς του δείχνοντας το συνδυασμό συνθηκών για τις οποίες η Χ έχει μια θετική επίδραση στην Υ καθώς και το συνδυασμό συνθηκών όταν η Χ έχει μια αρνητική επίδραση στην Υ. Επιπλέον, στην πράξη, πολλές φορές, ανακαλύπτουμε ότι περισσότεροι από ένας συνδυασμός συνθηκών οδηγεί σε υψηλές (χαμηλές) τιμές στην εξαρτημένη μεταβλητή. Δηλαδή, η πραγματικότητα συνήθως υποδεικνύει ότι ένας συνδυασμός συνθηκών μπορεί να έχει μια ασύμμετρη σχέση με μια κατάσταση έκβασης (αποτέλεσμα) και όχι μια συμμετρική σχέση.

Ποιοτική Συγκριτική Ανάλυση (ΠΣΑ) με χρήση ασαφών συνόλων

Τη δεκαετία του 80’ προτάθηκε από τον Charles Ragin (1987), αρχικά, η ΠΣΑ (QCA), βασισμένη στην άλγεβρα Boole. Στόχος ήταν η ανάπτυξη μιας «σύνθετης στρατηγικής», μιας μεθόδου δηλαδή που θα κινείται ανάμεσα σε αυτές που προσανατολίζονται προς τις περιπτώσεις (case-oriented) ή ποιοτικές προσεγγίσεις (Ragin & Rihoux, 2004), αλλά και τις μεθόδους που προσανατολίζονται προς τις μεταβλητές (variable-oriented) ή ποσοτικές προσεγγίσεις. Δηλαδή, η ΠΣΑ ενσωματώνει τα καλύτερα χαρακτηριστικά των δύο παραπάνω προσεγγίσεων και επιδιώκει τη γεφύρωση του χάσματος μεταξύ τους. Τα πλεονεκτήματα της ΠΣΑ είναι η δυνατότητα να παράγει γενικεύσεις, η αναλυτική προσέγγιση που επιτρέπει την επανάληψη των αποτελεσμάτων και ο προσδιορισμός μη συμμετρικών σχέσεων συνόλων. Αρχικά η ερευνητική ανάπτυξη και η εφαρμογή της μεθόδου χρησιμοποιήθηκε στην κοινωνιολογία και την πολιτική επιστήμη. Ο Gerring (2001) επισημαίνει ότι η ΠΣΑ είναι μια από τις μεθοδολογικές καινοτομίες των τελευταίων δεκαετιών, αφού η μέθοδος βρήκε εφαρμογές σε διάφορους τομείς, όπως τη διοίκηση επιχειρήσεων, την πολιτική ανάλυση, τη διαχείριση καινοτομίας, την εκπαίδευση, τις επιστήμες περιβάλλοντος, την έρευνα για την υγεία, κλπ.

Οι βασικές αρχές της ΠΣΑ είναι δύο, η σύνθετη αιτιότητα και ο συνδυασμός λεπτομερών αναλύσεων, εντός των περιπτώσεων, με τυποποιημένες συγκρίσεις μεταξύ τους. Δηλαδή, ουσιαστικά η αρχική αυτή προσέγγιση προσπάθησε να καλύψει δύο φαινομενικά αντιφατικούς στόχους:

1. Ένα επίπεδο γενίκευσης για τη σαφέστερη κατανόηση των αιτιωδών σχέσεων που οδηγούν στην εμφάνιση του αποτελέσματος που εξετάζει ο ερευνητής.
2. Τη συγκέντρωση γνώσης για τις περιπτώσεις που εξετάζει ο ερευνητής (πχ. χώρες, εργαζόμενοι, καταναλωτές, επιχειρήσεις) παρουσιάζοντας την πολυπλοκότητά τους και εξετάζοντας τις ομοιότητες και τις διαφορές τους.

Αργότερα, τη δεκαετία του 90’, ο καθηγητής Ragin, επέκτεινε τη μέθοδο, στην ασαφή άλγεβρα μέσω της χρήσης των ασαφών συνόλων, στην fs/QCA, η οποία έγινε ευρύτερα γνωστή. Δηλαδή, η fs/QCA αποτελεί προέκταση της QCA. Τα ασαφή σύνολα επέτρεψαν στους ερευνητές να αναλύουν όχι μόνο διχοτομικές μεταβλητές, αλλά και ασαφείς μεταβλητές με βαθμολογίες συμμετοχής μέλους στο διάστημα μεταξύ 0 και 1. Γενικά, η fs/QCA είναι μια μέθοδος ανάλυσης συνόλων. Ο βασικός στόχος της είναι να ανακαλύψει όλες τις αναγκαίες και ικανές συνθήκες που οδηγούν στο αποτέλεσμα. Οι αναγκαίες συνθήκες είναι αυτές που ‘παράγουν’ το αποτέλεσμα. Ολες οι περιπτώσεις που εμφανίζουν ένα αποτέλεσμα, εμφανίζουν επίσης και τις αναγκαίες συνθήκες. Ωστόσο, οι αναγκαίες συνθήκες από μόνες τους δεν είναι πάντα αρκετές για την εμφάνιση ενός αποτελέσματος. Οι ικανές συνθήκες είναι αυτές που πάντα οδηγούν σε ένα συγκεκριμένο αποτέλεσμα, αν και αυτές μπορεί να είναι αρκετές. Για το μαθηματικό μοντέλο της μεθόδου ο αναγνώστης παραπέμπεται στα άρθρα των Mendel & Corjani (2012 a, b).

Περιληπτικά, τα βήματα που ακολουθεί η fs/QCA είναι:

1. Βαθμονόμηση ασαφών συνόλων
2. Ανάλυση αναγκαίων συνθηκών για τη παρουσία (απουσία) του αποτελέσματος
3. Πίνακας Αλήθειας (Δημιουργία και Boolean Ελαχιστοποίηση)
4. Ανάλυση ικανών συνθηκών για τη παρουσία (απουσία) αποτελέσματος
5. Αποτελέσματα (μονοπάτια-κανόνες της Σύνθετης, Φειδωλής και Ενδιάμεσης λύσης) καθώς και δείκτες συνέπειας και κάλυψης.

Για τη βαθμονόμηση των ασαφών συνόλων, η μέθοδος χρησιμοποιεί τη σιγμοειδή λογιστική συνάρτηση με τρία σημεία αποκοπής των συνόλων για «περισσότερο εντός», «περισσότερο εκτός» και το σημείο της μέγιστης ασάφειας (ή cross-over point = 0.5 για τις περιπτώσεις που δεν είναι ούτε εντός ούτε εκτός από το ασαφές σύνολο). Ωστόσο, ο ερευνητής για τη βαθμονόμηση μπορεί να χρησιμοποιήσει όποια άλλη συνάρτηση επιθυμεί. Γενικότερα ισχύει για τη βαθμονόμηση του αποτελέσματος και των αιτιωδών συνθηκών, όπου ο: output και i αιτιώδεις συνθήκες, and , x = 1,…, N.

΄Όσον αφορά τον πίνακα αλήθειας, αυτός αποτελεί ένα εργαλείο ανάλυσης που παρουσιάζει όλους τους πιθανούς συνδυασμούς των αιτιωδών συνθηκών (πχ. δεικτών, κριτηρίων, κλπ) καθώς και την κατανομή των περιπτώσεων που περιλαμβάνονται σε αυτούς τους συνδυασμούς. Το πλήθος των γραμμών του πίνακα αλήθειας ισούται με 2ⁿ, όπου nοι αιτιώδεις συνθήκες που ερευνώνται για την παρουσία (ή απουσία) του αποτελέσματος. Κάθε γραμμή αντιπροσωπεύει ένα συγκεκριμένο συνδυασμό των αιτιωδών συνθηκών, και ο πλήρης πίνακας παρουσιάζει όλους τους πιθανούς συνδυασμούς τους (αιτιώδεις συνδυασμοί). Οι περιπτώσεις που περιλαμβάνονται στο σύνολο των δεδομένων, ταξινομούνται στις γραμμές του πίνακα με βάση τις τιμές τους, κι έτσι προκύπτουν γραμμές που περιλαμβάνουν πολλές περιπτώσεις, άλλες γραμμές με λιγότερες και τέλος κάποιες γραμμές με καμία περίπτωση, ειδικά όταν στα δεδομένα δεν υπάρχει ο συγκεκριμένος συνδυασμός χαρακτηριστικών που να συνδέεται με το ζητούμενο αποτέλεσμα. Πριν από τη λογική ελαχιστοποίηση του αριθμού των γραμμών του πίνακα αλήθειας θα πρέπει να προσδιοριστούν 2 κατώφλια: (α) η συχνότητα που υποδεικνύει τον ελάχιστο αριθμό περιπτώσεων που απαιτούνται ώστε να εξετασθεί μια γραμμή του πίνακα αλήθειας. (β) Το ελάχιστο επίπεδο συνέπειας για να θεωρηθεί μια γραμμή του πίνακα (αιτιώδης συνδυασμός) συνεπές υποσύνολο του αποτελέσματος. Ο υπολογισμός της συνέπειας ουιαστικά υιοθετεί το μέτρο γειτονίας (subsethood formula) του Kosko (1992) για να καθορίσει το βαθμό που το Α σύνολο περιέχεται στο Β ή διαφορετικά το βαθμό που ένας αιτιώδης συνδυασμός είναι υποσύνολο του αποτελέσματος. Η συνέπεια των αιτιωδών συνδυασμών θα πρέπει να είναι υψηλότερη του κατωφλιού 0,80.

Για την ελαχιστοποίηση του πίνακα αλήθειας η μέθοδος χρησιμοποιεί τον αλγόριθμο των Queen-McClusky (1952, 1966), αν και για μικρά σύνολα δεδομένων ο ερευνητής μπορεί να χρησιμοποιήσει και τους Χάρτες Καρνώ (Karnaugh).

΄Όσον αφορά τις λύσεις, η μέθοδος προτείνει τρεις περιπτώσεις: τη Σύνθετη, τη Φειδωλή και την Ενδιάμεση λύση. Οι λύσεις ουσιαστικά αποτελούν εναλλακτικά μονοπάτια συνδυασμών των αιτιωδών συνθηκών για την παρουσία (ή την απουσία, συμπληρωματικό ασαφές σύνολο) του αποτελέσματος.

Συνολικά, η fsQCA ως εργαλείο ανάλυσης συμπληρώνει άλλες παραδοσιακές αναλύσεις με τρεις κυρίως τρόπους: (α) ασυμμετρία (οι σχέσεις μεταξύ ανεξάρτητων και εξαρτημένων μεταβλητών αντιμετωπίζονται ως μη συμμετρικές), (β) πολλαπλά μονοπάτια και λύσεις οδηγούν στο ίδιο αποτέλεσμα και (γ) αιτιακή πολυπλοκότητα. Έτσι, ο ερευνητής δεν επικεντρώνεται στην εκτίμηση των ανεξάρτητων καθαρών αποτελεσμάτων, αλλά στην εκτίμηση των συνδυαστικών επιδράσεων (Elliott, 2013).

Πιλοτική εφαρμογή: πτώχευση των επιχειρήσεων

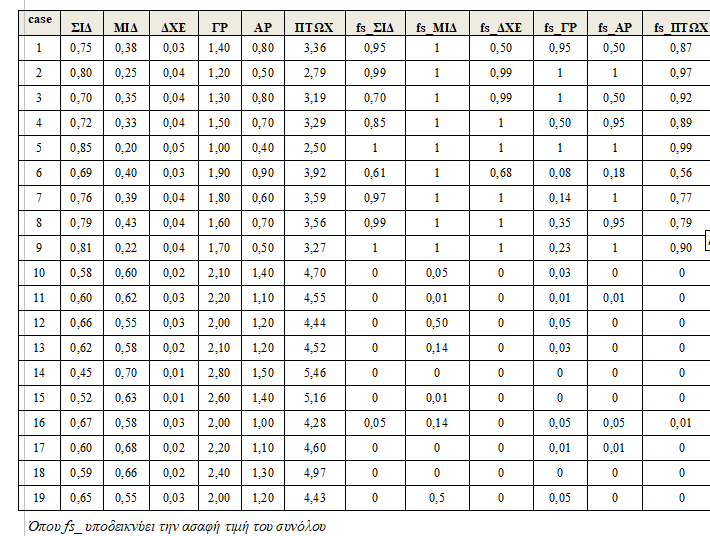
Η εφαρμογή έγινε σε πιλοτικό δείγμα 19 υγειών και μη υγειών επιχειρήσεων με γνώμονα πέντε χρηματοοικονομικούς δείκτες, οι οποίοι αποτελούν τις αιτιώδεις συνθήκες για το αποτέλεσμα (πτώχευση). Οι αιτιώδεις συνθήκες – δείκτες που χρησιμοποιήθηκαν είναι: η Συνολική Ικανότητα Δανεισμού (ΣΙΔ), η Μακροπρόθεσμη Ικανότητα Δανεισμού (ΜΙΔ), η Διαχείριση Χρηματοοικονομικών Εξόδων (ΔΧΕ), η Γενική Ρευστότητα (ΓΡ) και η Άμεση Ρευστότητα (ΑΡ). Ως μεταβλητή αποτελέσματος δημιουργήθηκε η μεταβλητή πτώχευσης (ΠΤΩΧ), ως άθροισμα των δεικτών. Οι επιδόσεις των επιχειρήσεων καθώς και τα ασαφή σύνολα που δημιουργήθηκαν, φαίνονται στον Πίνακα 1, ενώ οι τιμές των τριών κατωφλιών βαθμονόμησης εμφανίζονται στον Πίνακα 2.

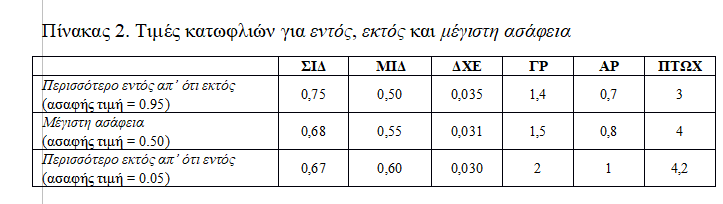
Σύμφωνα με τη βιβλιογραφία, ένας καλός δείκτης ΣΙΔ πρέπει να είναι μικρότερος ή ίσος του 67%, αντίστοιχα ένας καλός δείκτης ΜΙΔ μεγαλύτερος ή ίσος του 50%, ο δείκτης ΔΧΕ μικρότερος ή ίσος του 3%, ο δείκτης ΓΡ μεγαλύτερος ή ίσος του 2 και ο δείκτης ΑΡ μεγαλύτερος ή ίσος του 1.

Ως τιμές κατωφλιών για την περίπτωση εντός, εκτός και μέγιστης ασάφειας (βλ. Πίνακα 2), στον δείκτη ΣΙΔ χρησιμοποιήθηκαν οι τιμές 0,75, 0,68 και 0,67. Ομοίως, για τον δείκτη ΜΙΔ χρησιμοποιήθηκαν οι τιμές 0,50, 0,55 και 0,60, κ.ο.κ. Ετσι, για παράδειγμα για το ασαφές σύνολο των επιχειρήσεων με κακή επίδοση στο δείκτη ΣΙΔ, η επίδοση 0,75 ή υψηλότερα, βαθμονομείται με τιμή 0,95 έως 1, δηλαδή όπως στη 2^η επιχείρηση ο δείκτης ΣΙΔ = 0,80 αντιστοιχεί στην ασαφή τιμή 0,99 που υποδεικνύει μια σίγουρη συμμετοχή στο ασαφές σύνολο των κακών επιχειρήσεων. Ομοίως, μια επίδοση επιχείρησης στον δείκτη ΣΙΔ μεταξύ 0,68 και 0,75 βαθμονομείται με τιμή μεταξύ 0,50 και 0,95 που υποδεικνύει μια περίπτωση επιχείρησης ‘περισσότερο εντός απ’ ότι εκτός’ του ασαφούς συνόλου των επιχειρήσεων με κακή επίδοση. Τέτοια περίπτωση είναι για παράδειγμα η 4^η επιχείρηση με δείκτη ίσο με 0,72 που η ασαφής τιμή ισούται με 0,85. Επίσης, μια επίδοση επιχείρησης στο συγκεκριμένο δείκτη μεταξύ 0,68 και 0,67 υποδεικνύει μια επιχείρηση ‘περισσότερο εκτός απ’ ότι εντός’ του ασαφούς συνόλου των επιχειρήσεων με κακή επίδοση, και τέλος ένας δείκτης κάτω από 0,67 υποδεικνύει μια επιχείρηση που σίγουρα είναι εκτός του ασαφούς συνόλου των επιχειρήσεων με κακή επίδοση, όπως η 19^η με δείκτη = 0,65 και ασαφή τιμή ίση με 0.

΄Όσον αφορά τις επιδόσεις των επιχειρήσεων στον δείκτη ΜΙΔ, για παράδειγμα στη 2^η επιχείρηση με δείκτη 0,25 η ασαφής τιμή είναι 1, δηλαδή η επιχείρηση μετέχει σίγουρα στο ασαφές σύνολο των επιχειρήσεων με κακή επίδοση. Αντίστοιχα, η 18^η επιχείρηση με δείκτη ίσο με 0,66 λαμβάνει ασαφή τιμή 0 που υποδεικνύει ότι σίγουρα δεν μετέχει στο ασαφές σύνολο των κακών επιχειρήσεων. Ομοίως, ισχύει για όλα τα υπόλοιπα ασαφή σύνολα.

Με γνώμονα την ανάλυση στο μικρό αυτό σύνολο δεδομένων προκύπτουν οι αναγκαίες συνθήκες που ‘παράγουν’ την πτώχευση. Οι δείκτες αυτοί είναι η Συνολική Ικανότητα Δανεισμού (ΣΙΔ), η Μακροπρόθεσμη Ικανότητα Δανεισμού (ΜΙΔ) και ο Δείκτης Επίδοσης Διαχείρισης (ΔΧΕ). Δηλαδή, όταν υπάρχει πτώχευση, συνυπάρχουν ταυτόχρονα κακές επιδόσεις και στους τρεις αυτούς δείκτες.

Με γνώμονα την ελαχιστοποίηση του πίνακα αλήθειας των 2⁵=32 αιτιωδών συνδυασμών, και επιλέγοντας ως κατώφλια συχνότητας και συνέπειας το 1 και 0,80, αντίστοιχα, οι ικανές συνθήκες της πτώχευσης, σύμφωνα με τη Σύνθετη λύση, είναι δύο μονοπάτια (κανόνες). Δηλαδή, κάθε ένα μονοπάτι όταν συμβαίνει, εναλλακτικά, έχει ως αποτέλεσμα την πτώχευση. Σημειώνεται, ότι για ένα μικρό αρχείο δεδομένων, όπως το πιλοτικό της παρούσας εφαρμογής, η Σύνθετη λύση προτείνεται ως η αντιπροσωπευτικότερη μεταξύ Φειδωλής και Ενδιάμεσης. Ειδικότερα, τα μονοπάτια της Σύνθετης λύσης, όπου οι αιτιώδεις συνθήκες συνδέονται με το λογικό AND και τα μονοπάτια μεταξύ τους με το λογικό OR, είναι τα εξής:

1. Παρουσία ενός κακού δείκτη ΣΙΔ & ταυτόχρονα παρουσία ενός κακού δείκτη ΜΙΔ & ταυτόχρονα παρουσία ενός κακού δείκτη ΔΧΕ & ταυτόχρονα απουσία ενός κακού δείκτη ΓΡ, ανεξάρτητα εάν ο δείκτης ΑΡ λαμβάνει καλές ή κακές τιμές.

1. Παρουσία ενός κακού δείκτη ΣΙΔ & ταυτόχρονα παρουσία ενός κακού δείκτη ΜΙΔ & ταυτόχρονα παρουσία ενός κακού δείκτη ΔΧΕ & ταυτόχρονα παρουσία ενός κακού δείκτη ΑΡ, ανεξάρτητα εάν ο δείκτης ΓΡ λαμβάνει καλές ή κακές τιμές.

Υπό μορφή κανόνα τα παραπάνω μονοπάτια μπορούν να διατυπωθούν ως εξής:

• EAN ταυτόχρονα κακοί δείκτες ΣΙΔ, ΜΙΔ, ΔΧΕ και όχι κακός δείκτης ΓΡ, ΤΟΤΕ πτώχευση,ή εναλλακτικά,
• ΕΑΝ ταυτόχρονα κακοί δείκτες ΣΙΔ, ΜΙΔ, ΔΧΕ, ΑΡ, ΤΟΤΕ πτώχευση.

Χωρίς να αναλυθούν επιμέρους τεχνικά θέματα, το πρώτο μονοπάτι – κανόνας από τα δύο παραπάνω είναι ‘καλύτερο’ του δεύτερου. Δηλαδή, επεξηγεί καλύτερα τα δεδομένα του συνόλου δεδομένων.

Συνολικά, η λύση των δύο μονοπατιών είναι αρκετά συνεπής (συνολικός δείκτης συνέπειας = 0,93, ανάλογος του R² στην παλινδρόμηση) και η λύση συνολικά δείχνει πολύ υψηλή κάλυψη των δεδομένων, συνολικός δείκτης κάλυψης = 0,89 (η κάλυψη δείχνει πόσο καλά επεξηγείται η πτώχευση από τις 2 λύσεις – μονοπάτια).

Πίσω από αυτή την πρώτη ‘ανάγνωση’ των αριθμών, κρύβονται πολλά τεχνικά θέματα, τα οποία δεν είναι της παρούσης. Σίγουρα όμως οι αριθμοί αυτοί δίνουν ένα αποτέλεσμα των συνδυασμών των αιτιωδών συνθηκών (δεικτών) που οδηγούν στο αποτέλεσμα (πτώχευση). Αξίζει να τονίσομε ότι τα αποτελέσματα αυτά αφορούν το συγκεκριμένο σύνολο δεδομένων, δηλαδή η μέθοδος επιδιώκει να περιγράψει (όχι να προβλέψει) τι κρύβουν οι αριθμοί.

Συμπερασματικά επισημαίνεται η χρησιμότητα της fs/QCA για τον εντοπισμό των μονοπατιών, τα οποία περιλαμβάνουν διαφορετικούς συνδυασμούς συνθηκών για να πραγματοποιηθεί η πτώχευση. Η εφαρμογή της fs/QCA μπορεί να συμπληρώσει αναλύσεις που πραγματοποιούνται με τις συνηθισμένες ποσοτικές τεχνικές για τον εντοπισμό της σύνθετης αιτιότητας, ισοδύναμων λύσεων και την εξέταση των μη συμμετρικών σχέσεων. Τέλος, η fs/QCA αποτελεί ένα πολύτιμο αναλυτικό εργαλείο για την ανάπτυξη πληρέστερων ερμηνειών.

Βιβλιογραφία

Ζοπουνίδης Κ. (2013). Βασικές αρχές Χρηματοοικονομικού Μάνατζμεντ, Εκδ. Κλειδάριθμος.

Elliott, T. (2013). Fuzzy set qualitative comparative analysis: An introduction. Research notes, Statistics Group: UCl.

Gerring, J. (2001). Social science methodology: A critical framework. Cambridge, UK: Cambridge University Press.

Kosko, B. (1986). Entropy and Conditioning, Information Sciences, 40, pp. 165-174.

McCluskey, E.J. (1966). Introduction to the Theory of Switching Circuits. McGraw-Hill, New York.

Mendel, J.M., Korjani M.M. (2012a). Charles Ragin’s Fuzzy Set Qualitative Comparative Analysis (fsQCA) used for linguistic summarizations. Information Sciences, 202, pp. 1-23.

Mendel J.M., Korjani M.M. (2012b). Fast Fuzzy Set Qualitative Comparative Analysis (Fast fsQCA), Conference Paper in Studies in Fuzziness and Soft Computing, IEEE, DOI: 10.1109/NAFIPS.2012.6291025, August 2012.

Quine, W.V. (1952). The problem of simplifying truth functions. American Mathematical Monthly, 59, 521– 531.

Ragin, C. C. (1987). The comparative method. Moving beyond qualitative and quantitative strategies, Berkeley, Los Angeles & London: University of California Press.

Ragin, C. C. (2000) Fuzzy-set social science. Chicago: Chicago University Press.

Ragin, C. C. (2008). Redesigning social inquiry: Fuzzy sets and beyond. Chicago: Chicago University Press.

Ragin, C. C. and Rihoux, B. (2004) ‘Qualitative Comparative Analysis (QCA): State of the Art and Prospects’, Qualitative Methods: Newsletter of the American Political Science Association Organized Section on Qualitative Methods, 2(2): 3–13.

Quine, W.V. (1952). The problem of simplifying truth functions. American Mathematical Monthly, 59, 521– 531.

McCluskey, E.J. (1966). Introduction to the Theory of Switching Circuits. McGraw-Hill, New York.

Woodside, A. (2013). Moving beyond multiple regression analysis to algorithms: Calling for adoption of a paradigm shift from symmetric to asymmetric thinking in data analysis and crafting theory. Journal of Business Research, 66(4), 463-472.