Η διαδικασία διαχείρισης χαρτοφυλακίων αποτελεί μια ολοκληρωμένη δυναμική ακολουθία βημάτων η οποία στοχεύει στην επιλογή κατάλληλων συνδυασμών χρεογράφων, με βάση το προφίλ και τις προκαθορισμένες απαιτήσεις κάθε επενδυτή. (βλ. Ξυδώνας, Ψαρράς, Ζοπουνίδης, Σύγχρονη Θεωρία Χαρτοφυλακίου, Εκδ. Κλειδάριθμος, 2010).
Γράφει ο Καθηγητής Κωνσταντίνος Ζοπουνίδης, Ακαδημαϊκός, Βασιλική Ακαδημία Οικονομικών και Χρηματοοικονομικών, Βασιλική Ευρωπαϊκή Ακαδημία των Διδακτόρων, Πολυτεχνείο Κρήτης & Audencia Business School, France
Η θεωρία χαρτοφυλακίου αναπτύχθηκε για πρώτη φορά από τον Harry Markowitz με τη δημοσίευση του άρθρου “Portfolio Selection”, στο έγκυρο περιοδικό “The Journal of Finance” το 1952. Οι βασικές αρχές αυτού του μοντέλου διευκολύνουν την επιλογή αποτελεσματικών χαρτοφυλακίων. Σύμφωνα με τις αρχές αυτές, ο επενδυτής που επιθυμεί να μεγιστοποιήσει τα εισοδήματά του από το χαρτοφυλάκιο που κατέχει, οφείλει να γνωρίζει το μέσο (αναμενόμενη απόδοση) και τη διακύμανση ή τυπική απόκλιση (κίνδυνος) αυτού του χαρτοφυλακίου. Στο άρθρο αυτό θα παρουσιαστεί η μέθοδος του μέσου-διακύμανσης (Mean – Variance) για την αξιολόγηση ενός χαρτοφυλακίου δύο περιουσιακών στοιχείων.
Υπολογισμός Μέσου – Διακύμανσης
Τα περιουσιακά στοιχεία δεν είναι μεμονωμένα, αλλά διατηρούνται μαζί με άλλα περιουσιακά στοιχεία. Έτσι η επικινδυνότητα ενός περιουσιακού στοιχείου μπορεί να επηρεαστεί από την αλληλεπίδραση της διάρθρωσης των αποδόσεών του με εκείνη των αποδόσεων των άλλων περιουσιακών στοιχείων.
Θεωρούνται δύο επικίνδυνα χρεόγραφα (μετοχές) Χ και Y που έχουν κανονικές κατανομές πιθανοτήτων. Τα κεφάλαια που επενδύονται κατανέμονται με τον ακόλουθο τρόπο:
a% στο χρεόγραφο Χ
b% = (1 – a%) στο χρεόγραφο Y.
Με τα παραπάνω δεδομένα είναι δυνατόν τώρα να υπολογιστούν ο μέσος (αναμενόμενη απόδοση) και η τυπική απόκλιση (κίνδυνος) του χαρτοφυλακίου των δύο επικίνδυνων χρεογράφων.
Η αναμενόμενη απόδοση του χαρτοφυλακίου είναι η ακόλουθη:
Ε(Rp) = Ε[aX + bΥ]
ή Ε(Rp) = Ε(aX) + Ε(bY)
και τελικά
Ε(Rp) = aΕ(X) + bΕ(Y) (1)
Η διακύμανση του χαρτοφυλακίου υπολογίζεται με τον ακόλουθο τρόπο:
VAR(Rp)=Ε[Rp – Ε(Rp)]2 = Ε[(aX + bY) – E(aX + bY)]2
γνωρίζοντας ότι Rp =aX + bY
Μετά από υπολογισμούς η εξίσωση διαμορφώνεται ως εξής:
VAR(Rp) = E[(aX – aE(X)) + (bY – bE(Y))]2
ή VAR(Rp) = E[a2(X – E(X))2 + b2(Y – E(Y))2 + 2ab(X – E(X))(Y – E(Y))]
Σύμφωνα με τους ορισμούς της στατιστικής πραγματοποιούνται οι ακόλουθες μετατροπές:
a2E[(X – E(X))2] = VAR(aX) = a2VAR(X)
b2E[(Y – E(Y))2] = VAR (bY) = b2VAR(Y)
E[(X – E(X))(Y – E(Y))] = COV(X, Y)
και τελικά
VAR(Rp) = a2VAR(X) + b2VAR(Y) + 2abE[(X – E(X))(Y – E(Y))]
ή
VAR(Rp) = a2VAR(X) + b2VAR(Y) + 2abCOV(X, Y) (2)
Η συνδιακύμανση δείχνει τη διεύθυνση την οποία ακολουθούν οι αποδόσεις των δύο χρεογράφων. Όταν είναι θετική, τα δύο χρεόγραφα ακολουθούν την ίδια διεύθυνση, ενώ όταν είναι αρνητική, τα δύο χρεόγραφα ακολουθούν αντίθετες διευθύνσεις. Η συνδιακύμανση είναι μια βασική έννοια διότι εξετάζει τη συνεισφορά κάθε χρεογράφου στο συνολικό κίνδυνο του χαρτοφυλακίου χρεογράφων.
Παράδειγμα
Δίδονται στον παρακάτω πίνακα οι αποδόσεις των χρεογράφων Χ και Υ καθώς επίσης και οι πιθανότητες πραγματοποίησης τους.
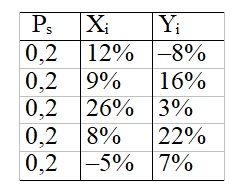
E(X) = 0,2(0,12) + 0,2(0,09) + 0,2(0,26) + 0,2(0,08) – 0,2(0,05) = 0,1 = 10,0%Η εφαρμογή των τύπων (1) και (2) και της συνδιακύμανσης δίνουν τα ακόλουθα αποτελέσματα για κάθε χρεόγραφο.
E(Y) = –0,2(0,08) + 0,2(0,16) + 0,2(0,03) + 0,2 (0,22) + 0,2(0,07) = 0,08 = 8,0%
VAR(X) = 0,2(0,12–0,10)2 + 0,2(0,09–0,10)2 + 0,2(0,26–0,10)2 + 0,2(0,08–0,10)2 + 0,2(–0,05–0,10)2 = 0,0058
VAR(Y) = 0,2(–0,08–0,08)2 + 0,2(0,16–0,08)2 + 0,2(0,03–0,08)2 + 0,2(0,22–0,08)2 + 0,2(0,07–0,08)2 = 0,0108
COV(X,Y) = 0,2(0,12–0,10) (–0,08–0,08) + 0,2(0,09–0,10) (0,16–0,08) + 0,2(0,26–0,10) (0,03–0,08) + 0,2(0,08–0,10) (0,22–0,08) + 0,2(–0,05–0,10) (0,07–0,08) = –0,0015
Η αρνητική τιμή της συνδιακύμανσης σημαίνει ότι οι αποδόσεις των δύο χρεογράφων ακολουθούν αντίθετες διευθύνσεις.
Έστω τώρα ένας επενδυτής ο οποίος επενδύει 50% των κεφαλαίων του στο χρεόγραφο Χ και το υπόλοιπο 50% στο χρεόγραφο Υ. Να υπολογιστούν η αναμενόμενη απόδοση και ο κίνδυνος του χαρτοφυλακίου των δύο χρεογράφων. Η χρησιμοποίηση των τύπων δίνει τα ακόλουθα αποτελέσματα.
E(Rp) = 0,5(0,10) + 0,5(0,08) = 0,09 = 9,0%
VAR(Rp) = (0,5)2(0,0058) + (0,5)2(0,0108) + 2(0,5)(0,5)(–0,0015) = 0,0034
ή σ(Rp) = 5,83%.
Το πλεονέκτημα της διαφοροποίησης του χαρτοφυλακίου φαίνεται καθαρά με το παράδειγμα αυτό (η διαφοροποίηση επιφέρει αισθητή μείωση του κινδύνου).
Υπάρχουν βέβαια και άλλοι συνδυασμοί των χρεογράφων Χ και Υ που σχηματίζουν χαρτοφυλάκια. Ο παρακάτω πίνακας παρουσιάζει την αναμενόμενη απόδοση και τον κίνδυνο αυτών των χαρτοφυλακίων.
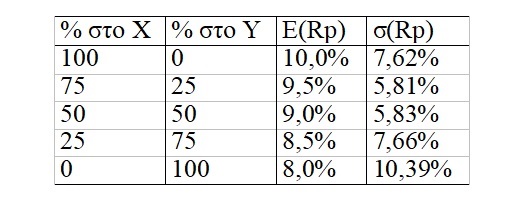
Πριν προσδιοριστεί το άριστο χαρτοφυλάκιο, θα μελετηθεί ο συντελεστής συσχέτισης των αποδόσεων των δύο χρεογράφων.Παρατηρείται ότι ο κίνδυνος του χαρτοφυλακίου μειώνεται μέχρι ενός ποσοστού a που επενδύεται στο χρεόγραφο Χ και στη συνέχεια αυξάνεται εκ νέου. Το άριστο ποσοστό a που θα προσδιορίσει το άριστο χαρτοφυλάκιο κυμαίνεται από 50% έως 75%.
Ο συντελεστής συσχέτισης ορίζεται από τη σχέση:
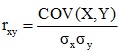
Αν οι αποδόσεις των δύο χρεογράφων είναι ανεξάρτητες, δηλαδή αν η συνδιακύμανση είναι ίση με μηδέν, τότε ο συντελεστής συσχέτισης είναι ίσος με μηδέν. Το Σχήμα 1 παρουσιάζει τις ανεξάρτητες αποδόσεις δύο χρεογράφων Α και Β.
Αν οι αποδόσεις των δύο χρεογράφων είναι τέλεια συσχετισμένες (perfectly correlated), τότε ο συντελεστής συσχέτισης είναι ίσος με +1 (βλ. Σχήμα 2, οι αποδόσεις βρίσκονται πάνω σε μια ευθεία γραμμή).
Το εύρος των τιμών για το συντελεστή συσχέτισης είναι εξομαλυμένο και περιορίζεται μεταξύ –1 και +1.
–1 rxy 1 (4)
Η γενική έκφραση για τη συνδιακύμανση μεταξύ δύο χρεογράφων είναι ο ακόλουθος τύπος:
COV(X,Y) = rxyσxσy
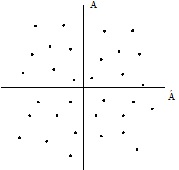
Σχήμα 1: Ανεξάρτητες αποδόσεις δύο χρεογράφων
Σχήμα 2: Τέλεια συσχετισμένες αποδόσεις δύο χρεογράφων
Η τοποθέτηση του τύπου (5) στον τύπο (2),ορίζει εκ νέου τη διακύμανση του χαρτοφυλακίου.
VAR(Rρ) = a2VAR(X) + b2VAR(Y) + 2abrxyσxσy (6)
Είναι δυνατόν τώρα να υπολογιστεί ο συντελεστής συσχέτισης των δύο χρεογράφων Χ και Υ.

Προσδιορισμός άριστου χαρτοφυλακίου με ελαχιστοποίηση της διακύμανσης
Το πρόβλημα συνίσταται εδώ στον υπολογισμό του άριστου ποσοστού a που επενδύεται στο χρεόγραφο Χ ώστε να αποκτηθεί το χαρτοφυλάκιο με την ελάχιστη διακύμανση (minimum variance portfolio).
Η ελαχιστοποίηση της διακύμανσης του χαρτοφυλακίου πραγματοποιείται υπολογίζοντας την πρώτη παράγωγο που είναι ίση με μηδέν.
Ο μαθηματικός τύπος της διακύμανσης του χαρτοφυλακίου μπορεί να γραφεί με τον ακόλουθο τρόπο:
VAR(Rp) = a2σ2x + (1 – a)2σ2y + 2a(1 – a)rxyσxσy
με b = 1 – a
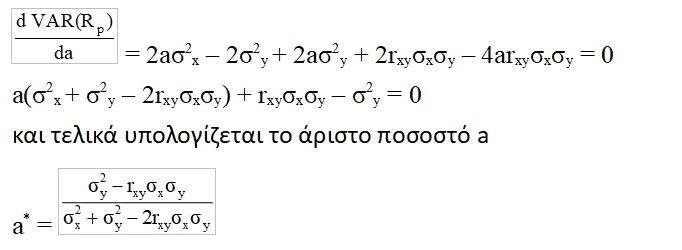
και τελικά υπολογίζεται το άριστο ποσοστό a
Για το προηγούμενο παράδειγμα η εφαρμογή του παραπάνω τύπου δίνει το ακόλουθο αποτέλεσμα.

Υπολογίζεται εκ νέου η αναμενόμενη απόδοση και η διακύμανση του χαρτοφυλακίου.
E(Rp) = 0,679(0,10) + 0,321(0,08) = 9,358%
VAR(Rp) = (0,679)2(0,0058) + (0,321)2(0,0108) +
+ 2(0,679)(0,321)(–0,19)(0,0762)(0,1039) = 0,00313114
σ(Rρ) = 5,595%.
Το χαρτοφυλάκιο με την ελάχιστη διακύμανση βρίσκεται στη συμβολή των δύο διακεκομμένων ευθειών (βλ. Σχήμα 3)
Όταν το χαρτοφυλάκιο αποτελείται από δύο χρεόγραφα, όλοι οι δυνατοί συνδυασμοί των δύο χρεογράφων βρίσκονται πάνω στην καμπύλη του σχήματος 3.
Η συνεχής καμπύλη (συνεχής γραμμή) δείχνει την αποτελεσματική περιοχή πάνω στην οποία βρίσκονται αποτελεσματικά χαρτοφυλάκια. Η διακεκομμένη καμπύλη έχει χαρτοφυλάκια που κυριαρχούνται από τα χαρτοφυλάκια της αποτελεσματικής περιοχής (για ένα ίδιο επίπεδο κινδύνου, τα χαρτοφυλάκια της αποτελεσματικής περιοχής έχουν μεγαλύτερη απόδοση). Το Σχήμα 4 παρουσιάζει καθαρά την ανωτερότητα του χαρτοφυλακίου P2 από το χαρτοφυλάκιο P1.
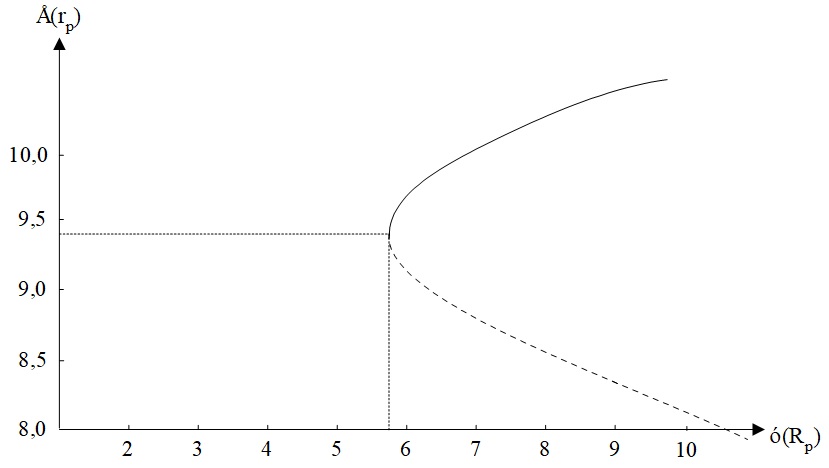
Σχήμα 3: Το χαρτοφυλάκιο δύο χρεογράφων με την ελάχιστη διακύμανση
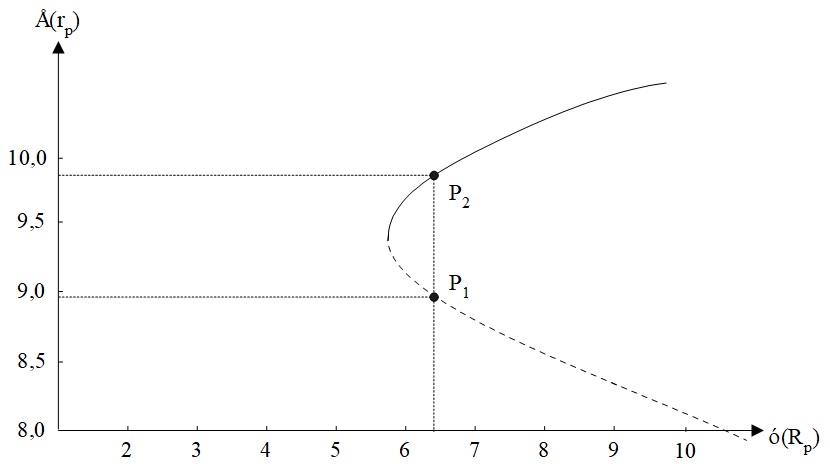
Σχήμα 4: Το χαρτοφυλάκιο P2 υπερέχει του χαρτοφυλακίου P1
Σε επόμενο άρθρο μας θα παρουσιάσουμε το υπόδειγμα αποτίμησης κεφαλαιουχικών περιουσιακών στοιχείων, το λεγόμενο Capital Asset Pricing Model-CAPM.



















