Τα κριτήρια εκτίμησης των επενδυτικών έργων υπό πιθανολογικό μέλλον
Το μέλλον είναι πιθανολογικό όταν τα διοικητικά στελέχη των επιχειρήσεων είναι ικανά να εκφράσουν υπό μορφή πιθανοτήτων τις διάφορους παραμέτρους υπολογισμού της επένδυσης.
Προηγουμένως, ο χρησιμοποιούμενος κανόνας απόφασης ήταν ο ακόλουθος: κάθε επενδυτικό έργο του οποίου η αποδοτικότητα ήταν μεγαλύτερη από το επιτόκιο προεξόφλησης k, ήταν αποδοτικό και όφειλε να πραγματοποιηθεί από την επιχείρηση.
Γράφει ο Καθηγητής Κωνσταντίνος Ζοπουνίδης, Ακαδημαϊκός, Βασιλική Ακαδημία Οικονομικών και Χρηματοοικονομικών, Βασιλική Ευρωπαϊκή Ακαδημία των Διδακτόρων, Πολυτεχνείο Κρήτης & Audencia Business School, France
Σε αβέβαιο μέλλον και μάλιστα πιθανολογικό, αυτός ο κανόνας δεν είναι απλός. Η αβεβαιότητα που αφορά κάθε παράμετρο υπολογισμού της επένδυσης προκαλεί μια μεταβλητότητα του αναμενόμενου αποτελέσματος και δημιουργεί στην επιχείρηση ένα κίνδυνο, όπως ο κίνδυνος που συνδέεται με ανεπιθύμητα αποτελέσματα.
Ο μάνατζερ της επιχείρησης, απέναντι στην αβεβαιότητα, μπορεί να αντιδράσει με τους δύο ακόλουθους τρόπους:
- είτε, για να περιορίσει την αβεβαιότητα και τον κίνδυνο που πηγάζει από αυτήν, ο μάνατζερ θα προσπαθήσει να αποκτήσει περισσότερη πληροφορία (προσθετική πληροφορία). Ένας ορθολογικός τρόπος για να αποκτηθεί αυτή η πληροφορία είναι, όταν αυτό είναι δυνατό, να μεγαλώσει η περίοδος πραγματοποίησης του επενδυτικού έργου διαιρώντας το σε μικρές υποπεριόδους και πραγματοποιώντας το πολλές φορές. Με τον τρόπο αυτό ο μάνατζερ αντικαθιστά μια στιγμιαία απόφαση της επένδυσης με μια σειρά διαδοχικών αποφάσεων επένδυσης οι οποίες παίρνονται σε διαφορετικές στιγμές μέσα στο χρόνο.
- είτε, μη δυνάμενος να περιορίσει την αβεβαιότητα και τον κίνδυνο, ο μάνατζερ της επιχείρησης, πριν αποφασίσει να επενδύσει, θα εκτιμήσει τον κίνδυνο και θα καλυφθεί στην συνέχεια έναντι αυτού.
Περιπτώσεις στιγμιαίων Αποφάσεων επένδυσης
Θα εξεταστεί η αναλυτική μέθοδος του Hillier, The Derivation of Probabilistic Information for the Evaluation of Risky Investments, Management Science, 1969, 443-457.
Παρουσίαση της μεθόδου
Ο Hillier θεωρεί ένα επενδυτικό έργο του οποίου κάθε μια από τις καθαρές ταμειακές ροές Χ0 ,Χ1, Χ2, …, Χt,…ΧΤ (t = 1, 2, …, T) 1, υποτίθεται ότι ακολουθεί μια κανονική κατανομή με μέσο μt και τυπική απόκλιση σt.
Υπολογίζεται η ΚΠΑ του έργου.
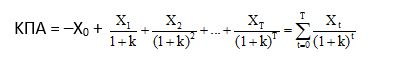
Επειδή όμως η μεταβλητή Xt μπορεί να πάρει πολλές τιμές, η ΚΠΑ του έργου μπορεί με τη σειρά της να πάρει και αυτή πολλές τιμές. Το σύνολο όμως των δυνατών τιμών που μπορεί να πάρει η ΚΠΑ του έργου ανήκουν σε μια στατιστική κανονική κατανομή μαθηματικής ελπίδας Ε(ΚΠΑ) και διακύμανσης V(ΚΠΑ).
Υπολογισμός της μαθηματικής ελπίδας Ε(ΚΠΑ) της κατανομής των δυνατών αποδόσεων
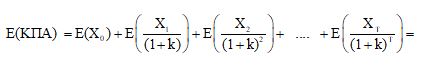
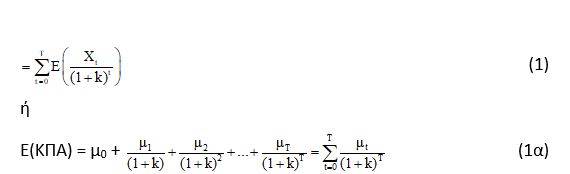
Η μαθηματική ελπίδα της ΚΠΑ είναι ίση με το άθροισμα των μαθηματικών ελπίδων των κάθε μια από τις ταμειακές ροές.
Υπολογισμός της διακύμανσης V(ΚΠΑ) της κατανομής των δυνατών αποδόσεων
Ο υπολογισμός της διακύμανσης V(ΚΠΑ) προϋποθέτει την εξέταση του βαθμού εξάρτησης των διαδοχικών καθαρών ταμειακών ροών του επενδυτικού έργου.
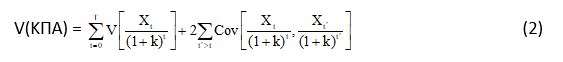
Η εξίσωση (2) εφαρμόζεται στο ακόλουθο επενδυτικό έργο:
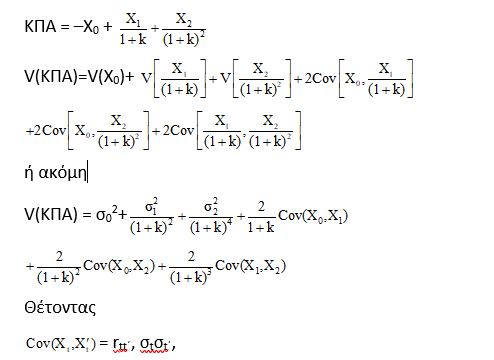
η παραπάνω εξίσωση διαμορφώνεται ως εξής:
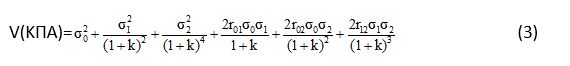
Η εξίσωση (3) δείχνει με τη βοήθεια των συντελεστών συσχέτισης rtt΄ το βαθμό συσχέτισης των καθαρών ταμειακών ροών του επενδυτικού έργου.
Ο Hillier, στο σημείο αυτό, θεωρεί τρεις βασικούς τύπους συσχετίσεων των καθαρών ταμειακών ροών:
- Οι καθαρές ταμειακές ροές είναι αμοιβαίως ανεξάρτητες (οριακή θέση)
- Οι καθαρές ταμειακές ροές είναι τέλεια συσχετισμένες μεταξύ τους (οριακή θέση)
- Οι καθαρές ταμειακές ροές δεν είναι ολικώς ανεξάρτητες ούτε τέλεια συσχετισμένες μεταξύ τους (πραγματική θέση).
1η περίπτωση: οι καθαρές ταμειακές ροές είναι αμοιβαίως ανεξάρτητες
Στην περίπτωση αυτή το σύνολο των rtt΄ είναι ίσο με μηδέν. Η εξίσωση (3) διαμορφώνεται ως εξής:

για το παραπάνω παράδειγμα και γενικά ο τύπος είναι
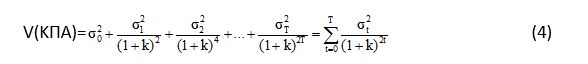
2η περίπτωση: Οι καθαρές ταμειακές ροές είναι τέλεια συσχετισμένες
Το σύνολο των rtt΄ είναι ίσο με +1. Η εξίσωση (3) γίνεται λοιπόν
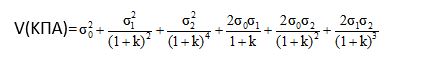
για το παράδειγμα και γενικά ο τύπος είναι
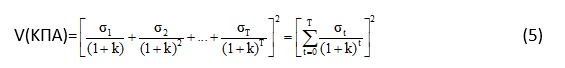
3η περίπτωση: Οι καθαρές ταμειακές ροές είναι εξαρτημένες αλλά όχι τέλεια συσχετισμένες (ρεαλιστική περίπτωση)
Η περίπτωση αυτή είναι η πιο ρεαλιστική αλλά και η πιο δύσκολη για να αναλυθεί. Η εξίσωση (3) πρέπει να χρησιμοποιηθεί για τον υπολογισμό της διακύμανσης της κατανομής. Αυτό βέβαια απαιτεί τον υπολογισμό των rtt΄ της εξίσωσης (3) ή των συνδιακυμάνσεων της εξίσωσης (2). Hillier αναγνωρίζει τη δυσκολία των υπολογισμών και προτείνει να απλοποιήσει το αρχικό μοντέλο. Δέχεται λοιπόν ότι οι καθαρές ταμειακές ροές Xt, που δεν είναι αμοιβαία ανεξάρτητες ούτε τέλεια συσχετισμένες μεταξύ τους, δύνανται όμως ατομικά να θεωρηθούν ως το αποτέλεσμα αθροίσματος δύο τυχαίων μεταβλητών Yt και Zt που ακολουθούν επίσης μια κανονική κατανομή (N(μt΄, σt΄) για Yt και (N(μt΄΄ , σt΄΄) για Zt). Οι μεταβλητές Yt θα είναι αμοιβαίως ανεξάρτητες ενώ οι μεταβλητές Zt θα είναι τέλεια συσχετισμένες μεταξύ τους.
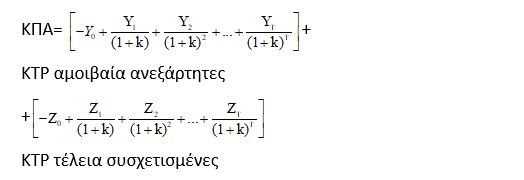
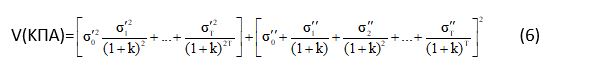
Ο πρώτος όρος της εξίσωσης (6) αντιστοιχεί στη διακύμανση που συνδέεται με τις ανεξάρτητες ταμειακές ροές (εξίσωση 4) και ο δεύτερος όρος αντιστοιχεί στη διακύμανση που συνδέεται με τις τέλεια συσχετισμένες καθαρές ταμειακές ροές (εξίσωση 5).
Στο τέλος αυτής της ανάλυσης υπάρχουν εκτιμήσεις για τις δύο παραμέτρους (μαθηματική ελπίδα και διακύμανση) οι οποίες επιτρέπουν στα διοικητικά στελέχη να γνωρίσουν τη μεταβλητότητα της απόδοσης του επενδυτικού έργου.
Εκτίμηση της μεθόδου
Οι κριτικές που αφορούν τη μέθοδο του Hillier είναι οι ακόλουθες:
- η υπόθεση της κανονικότητας της κατανομής των καθαρών ταμειακών ροών,
- η απλοποιημένη υπόθεση που θεωρεί ότι οι καθαρές ταμειακές ροές δεν είναι ολικά ανεξάρτητες ούτε τέλεια συσχετισμένες,
- το γεγονός ότι ο Hillier μελετά την αβεβαιότητα που συνδέεται με τις καθαρές ταμειακές ροές και υποθέτει έμμεσα ότι η διάρκεια χρήσης του εξοπλισμού είναι γνωστή.
3. Παράδειγμα
Η διοίκηση της επιχείρησης MASULIS μελετά το επενδυτικό έργο το οποίο έχει τα ακόλουθα χαρακτηριστικά:
Κατανομή των Καθαρών Ταμειακών Ροών
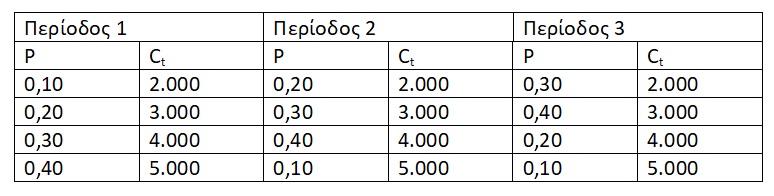
Η αρχική δαπάνη του επενδυτικού έργου είναι 8.000€ και το επιτόκιο προεξόφλησης είναι ίσο με 12%.
Ερωτήσεις
- Προσδιορίστε τη μαθηματική ελπίδα, τη διακύμανση και την τυπική απόκλιση του επενδυτικού έργου. Οι καθαρές ταμειακές ροές είναι ανεξάρτητες μεταξύ τους.
- Υπολογίστε την πιθανότητα ώστε το επενδυτικό έργο να έχει μια ΚΠΑ αρνητική ή ίση με μηδέν. Η ΚΠΑ ακολουθεί την κανονική κατανομή.
Λύση
1. Μαθηματική Ελπίδα, Διακύμανση, Τυπική Απόκλιση



2. Υπολογισμός Πιθανότητας

Άρα η πιθανότητα το επενδυτικό έργο να έχει μια ΚΠΑ αρνητική ή ίση με μηδέν είναι: 35,57%.



















